티스토리 뷰
1.8.1 전자와 정공의 농도
> 전자의 농도를 구하려면 전자가 있을 확률 (Fermi-Dirac 확률 분포)에 전자가 있을 모든 경우의 수 (Density Of State)를 곱에 에너지 범위만큼 적분하면 된다.
> 정공은 1 - 전자가 있을 확률에서 전자와 똑같이 Density Of State 곱하고 에너지 대역 만큼 적분하면 된다.
> 전자는 Ec~무한대 까지 적분, 정공은 가전자 대역 바닥~Ev까지의 적분하면 된다.
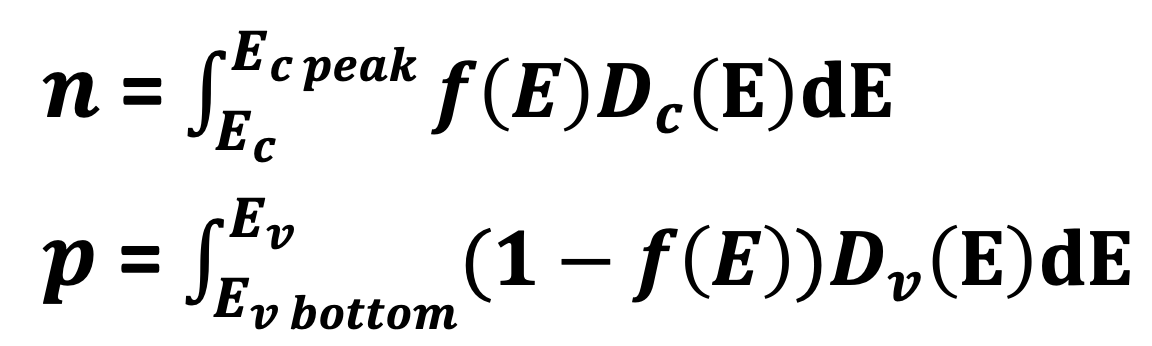
> 적분해서 구하면 Nc * exp, Nv * exp 값으로 얻어지는데 Nc, Nv를 유효 상태 밀도 (Effective Density of States) 한다.
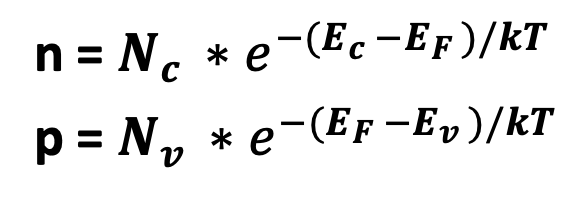
> 유효 상태 밀도의 의미는 E=Ec 일 때의 전자의 농도, E=Ev 일 때의 정공의 농도를 뜻 한다.
> Si의 Nc, Nv는 10^19 cm^-3 정도이고 유효 질량에 따라 다르다. (Table1)
| Ge | Si | GaAs | |
| Nc [〖cm〗^(-3)] | 1.04 × 10^19 | 2.8 × 10^19 | 4.7 × 10^17 |
| Nv [〖cm〗^(-3)] | 6.0 × 10^18 | 1.04 × 10^19 | 7.0 × 10^18 |
Table1. Effective Density Of States
1.8.2 페르미 준위와 캐리어 농도
> 전자의 농도가 높아질수록 Ef는 Ec에 가까워진다.
> 정공의 농도가 높아질수록 Ef는 Ev에 가까워진다.
> 온도가 높아질수록 Ef(Fermi Level)은 진성(Intrinsic) Si의 Ef에 가까워진다. (그림 1)
> 열적 평형 상태일 때 전자와 정공의 농도의 곱을 일정하다. np = ni^2 (mass action law).
> 주의할 점은 해당 관계는 E-Ef >> kT 조건에서만 성립된다, (Boltzmann Approximation)
> 그럼 불순물이 주입이 안되어 있는 Si이라면 생성되는 전자와 정공의 수는 동일하다.
> Valence Band에서 Conduction Band로 올라가는 전자는 정공을 발생시키기 때문이다.
> Doping이 되지 않은 Si을 진성 (Intrinsic) Si이라고 하고 n = p = ni(진성 케리어 농도)가 성립한다.
> Si의 ni는 10^10 개 정도이고 외워두면 좋다.
> N type 반도체에서 전자를 Majority Carrier, 정공을 Minority Carrier라 한다.
> P type은 N type의 반대이다.

1.8.1 Concentration of Electrons and Holes
> To determine the concentration of electrons, you can multiply the probability of having an electron (Fermi-Dirac probability distribution) by the total number of cases where electrons exist (Density of States), and then integrate over the energy range.
> For holes, subtract the probability of having an electron from 1, and then multiply it by the Density of States, integrating over the energy band.
> For electrons, integrate from Ec to infinity, and for holes, integrate from the valence band edge to Ev.
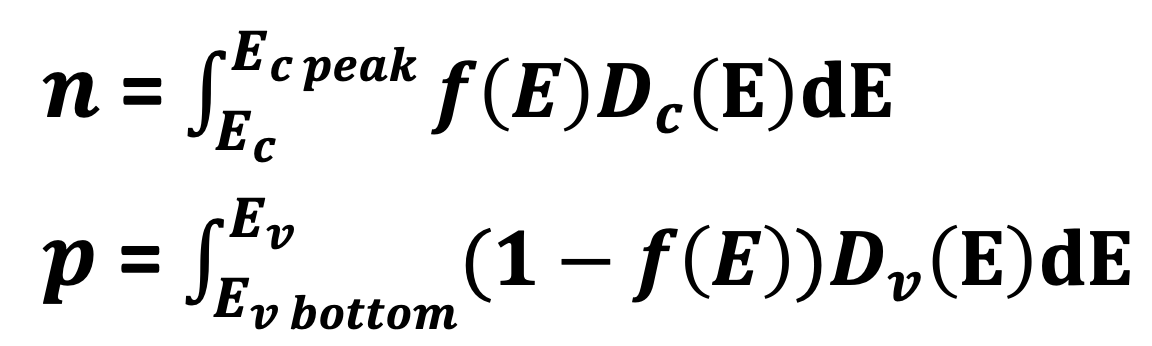
> The result of the integration gives you values in terms of Nc * exp and Nv * exp, where Nc and Nv are the Effective Density of States.
> The Effective Density of States signifies the concentration of electrons at E=Ec and the concentration of holes at E=Ev.
> The values for Nc and Nv in silicon (Si) are around 10^19 cm^-3, and they vary based on the effective mass. (See Table 1)
| Ge | Si | GaAs | |
| Nc [〖cm〗^(-3)] | 1.04 × 10^19 | 2.8 × 10^19 | 4.7 × 10^17 |
| Nv [〖cm〗^(-3)] | 6.0 × 10^18 | 1.04 × 10^19 | 7.0 × 10^18 |
Table1. Effective Density Of States
1.8.2 Fermi Level and Concentration of Carriers
> As the concentration of electrons increases, Ef moves closer to Ec.
> As the concentration of holes increases, Ef moves closer to Ev.
> At higher temperatures, Ef (Fermi Level) approaches the Ef of intrinsic silicon (Figure 1).
> In thermal equilibrium, the product of electron and hole concentrations remains constant: np = ni^2 (mass action law).
> Note that this relationship holds true only when E-Ef >> kT, known as the Boltzmann Approximation.
> If we consider undoped silicon (Si) without injected impurities, the number of generated electrons and holes will be equal.
> Electrons transitioning from the valence band to the conduction band create holes.
> Undoped Si is referred to as intrinsic Si, and n = p = ni (intrinsic carrier concentration) holds.
> The intrinsic carrier concentration of Si is approximately 10^10, and it's useful to remember.
> In N-type semiconductors, electrons are the majority carriers, and holes are the minority carriers.
> For P-type, it's the opposite of N-type.

Reference
-. Chenming Calvin Hu, Modern Semiconductor Devices for Integrated Circuits, PEARSON(2013)
'Semiconductor(반도체)' 카테고리의 다른 글
| 1.10 극고온과 극저온에서의 캐리어 농도 (Carrier Concentration at Extremely High and Low Temperatures) (0) | 2023.08.11 |
|---|---|
| 1.9 n과 p의 일반적 이론 (1) | 2023.08.10 |
| 1.7 열적 평형 상태와 페르미 함수(Thermal Equilibrium & Fermi Level) (0) | 2023.08.08 |
| 1.6 상태 밀도(Density of states) (0) | 2023.08.08 |
| 1.5 전자 및 정공(Electrons and Holes) (0) | 2023.08.06 |
- Total
- Today
- Yesterday
- channeling
- Charge Accumulation
- Optic Fiber
- PN Junction
- Fiber Optic
- EBD
- Blu-ray
- Pinch Off
- C언어 #C Programming
- 양자 웰
- Semicondcutor
- Thermal Noise
- 반도체
- semiconductor
- Solar cell
- Laser
- Donor
- 문턱 전압
- pn 접합
- fermi level
- Energy band diagram
- 쇼트키
- Acceptor
- 열전자 방출
- Diode
- CD
- MOS
- 광 흡수
- Depletion Layer
- Reverse Bias
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
