티스토리 뷰
1.7.1 열적 평형 상태
> 전자가 있을 확률을 이해하기 전에 열적 평형에 대한 개념이 필요하다.
> 진동 탁자 위에 모레가 쌓인 접시가 있다고 해보자.
> 탁자가 진동하면 모레도 진동하면서 고르게 펴지고 평탄한 표면이 만들어진다.
> 이 표면 상태는 외부로 받은 선동(agitation)으로 부터 최소 에너지 상태이며 평형 상태라고 한다.
> 전자가 존재할 확률은 페르미-디락 분포로 구할 수 있다.
1.7.2 페르미 레벨
> 페르미-디락 분포의 f(E)는 E 상태가 전자에 의해 점유될 확률이다.
> E가 충분히 큰 값을 가진다면 (E-Ef >> kT, Ef : fermi level, k : Boltzmann 상수, T : Temperature)
> 그 상태가 전자에 의해 점유될 확률 은 E가 증가할수록 지수함수적으로 감소한다.
> 좀 더 쉽게 말하면 에너지 대역이 높은 E에는 전자가 많이 없고 낮은 데는 많다. 즉 Ec 위에는 전자가 별로 없고 Ev에는 전자가 많다.
> f(E)는 전자가 있을 확률이고 Ef(페르미 레벨)는 전자가 있을 확률의 1/2 되는 에너지 준위이다.
> 여기서 열적 평형 상태가 중요한 이유가 나온다.
> 열적 평형 상태일 때 단 하나의 페르미 레벨이 존재한다.
> 이 개념은 EBD(Energy Band Diagram) 그릴 때 매우 중요한 개념으로 작용한다.
> 열적 평형 상태가 없으면 고려해야 할 것들이 많기 때문에 모델링을 간소화하기 위해 개념이 도입됐다고 생각하면 될 것 같다.
1.7.1 Thermal Equilibrium
> In order to know the presense of electrons, the concept of thermal equilibrium should be considered.
> Imagine a plate placed on a vibrating table
> It's evenly spread out due to the table's vibrations, achieving a flat surface.
> This state represents the lowest energy state resulting from external agitation and is referred to as equilibrium.
1.7.2 Fermi Level
> The Fermi-Dirac distribution allows us to deduce the probability of electron presence.
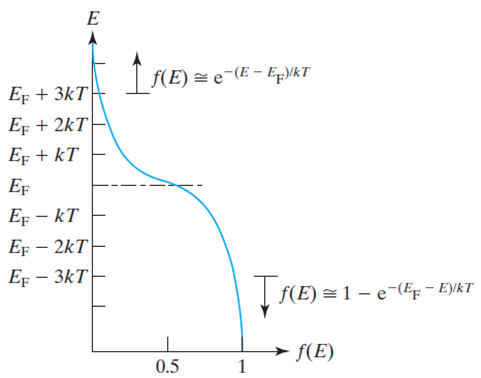
> In the Fermi-Dirac distribution, f(E) signifies the probability of an electron occupying the E state.
> When E has a significantly higher value (E - Ef >> kT, where Ef is the Fermi level, k is the Boltzmann constant, and T is temperature)
> The probability of occupation diminishes exponentially as E increases.
> Put simply, there are fewer electrons in higher energy states (above Ec) and more in lower energy states (in Ev).
> f(E) indicates the probability of electron presence, while Ef (Fermi level) marks the energy level where the probability of electron presence is 1/2.
> The significance of thermal equilibrium becomes evident here.
> In thermal equilibrium, only one Fermi level exists.
> This concept holds crucial importance when it comes to an Energy Band Diagram (EBD).
> Without thermal equilibrium, numerous complexities emerge, making the concept's introduction a way to streamline modeling.

Reference
-. Chenming Calvin Hu, Modern Semiconductor Devices for Integrated Circuits, PEARSON(2013)
-. 그림1 : Chenming Calvin Hu, Modern Semiconductor Devices for Integrated Circuits, PEARSON(2013), pg41
'Semiconductor(반도체)' 카테고리의 다른 글
| 1.9 n과 p의 일반적 이론 (1) | 2023.08.10 |
|---|---|
| 1.8 전자와 정공의 농도(Concentration of Carriers) (0) | 2023.08.09 |
| 1.6 상태 밀도(Density of states) (0) | 2023.08.08 |
| 1.5 전자 및 정공(Electrons and Holes) (0) | 2023.08.06 |
| 1.4 도체, 반도체, 절연체 (Conductor, Semiconductor, Insulator) (1) | 2023.08.06 |
- Total
- Today
- Yesterday
- Semicondcutor
- semiconductor
- EBD
- Reverse Bias
- Thermal Noise
- Pinch Off
- Solar cell
- channeling
- Diode
- Blu-ray
- Optic Fiber
- 쇼트키
- Energy band diagram
- pn 접합
- 반도체
- Charge Accumulation
- CD
- C언어 #C Programming
- Donor
- 광 흡수
- Depletion Layer
- PN Junction
- 양자 웰
- fermi level
- 열전자 방출
- MOS
- Fiber Optic
- Laser
- Acceptor
- 문턱 전압
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
