티스토리 뷰
최적화
> 선분은 시작과 끝 지점이 존재 (무한, 유한 차이)
> 선분의 어느 점을 표현할 때 w로 표현
> 직선의 범위는 무한, 직선을 포함하는 집합도 무한 이 집합을 아핀 셋이라고 한다.
> n차원으로 확장한 것을 아핀 조합이라고 한다
> 아핀 셋은 무한, 컨벡스 셋은 유한
> 컨벡스 셋은 선분을 포함한 유한 집합
> 회색 영역이 컨벡스 셋인가? 선분을 포함해야 함 (유한이어도)
> 찾는 solution의 범위가 컨벡스 셋이 아니면 거의 못 찾음
> 이차 함수 예제로 들었던 이유는 이차 함수가 컨벡스 셋이기 때문이다.
> 주어진 점들을 포함하는 컨벡스 셋을 의미
> w.T @ x 는 내적이고 내적 했을 때 스칼라 b를 갖는 벡터 x의 집합을 초평면이라고 한다.
> 원, 세모를 빨간 선을 기준으로 구분할 수 있다
> 여기서 빨간 선이 초평면
> 내적은 이동거리고 x, w의 내적 즉 이동거리인 b의 합이 빨간 선(초평면)
> w도 찾아야 되는 값
> 머신러닝은 초평면을 구하는 거고 여러 방법이 있고 잘 찾아야 한다
> w 는 x와 직교(orthogonal)한 특징을 갖는다
> 전체 공간은 두 개의 반공 간(halfsplce)으로 나뉨
> 반공간 구분은 내적을 해서 b를 넘는지 안 넘는지로 구분 가능
> 선분을 그었을 때 f의 함수 그래프보다 위에 있어야 한다
> 컨벡스 함수를 안 쓰면 여러 가지 증명을 해줘야 하기 때문에 하는 게 좋음
> 편미분의 집합
> 컨벡스이냐 아니냐를 따지는 케이스는 사실 많이 없음 (배우는 이론은 다 컨벡스이다)
> 머신러닝에서 최적화는 컨벡스 최적화이다.
> 최적화는 함수 f(x)의 최소값을 찾는 것
> x는 피쳐, f(x)는 타겟의 추정량
> 함수 f는 뭔지 모르지만 f(x)를 통해서 타겟 추정량이 나오면 타겟값과 비교한다.
> 타겟 y, 타겟 추정 y^ 차이를 오차, 머신 러닝에서 손실 Loss라고 표현한다
> 손실을 하나의 숫자로 표현은 1/n(sig(y-y^))이다.
> 평균이 들어가지 않아 분산은 아니고 이를 평균 오차 제곱 MSE라고 한다.
> MSE를 구해서 feature 타이 잘 만들었는지 확인할 수 있고 망소 항목이다.
> MSE가 거의 목적으로 되어 목적 함수이다.
> 목적함수가 MSE도 될 수 있고 다른 것도 될 수 있다.
> subject to 제약 조건
> 제약 조건 중 부등식, 등식 형태가 있을 수 있다. (상황에 따라 달라진다)
> 이전 내용은 일반적인 최적화
> f(x)는 목적함수이면서 컨벡스 함수여야한다. (선분이 함수보다 위에 있어야 함)
> 등식 부호 대신 내적값이 들어가 있고 초평면이 들어가 있다.
> 목적 함수와 제약 조건을 한 줄의 식으로 표현한게 라그랑주 프리멀 함수임
> 람다는 제약 조건을 얼마나 강하게 넣겠다라는 뜻, 0 이면 제약 조건이 없다
> 초평면을 구하는 방법은 라그랑주 프리멀 함수의 미분이 0 되는 지점을 구해서 그림
> 미분해서 0이라고 해서 최적점이 아닐 수 있다.
> 그래서 라그랑주 듀얼 함수도 봐줘야 한다
> 라그랑주 프리멀 함수의 하한이다.
> 예) 월급의 하한은 최저시급
> 라그랑주 프리멀과 듀얼 함수의 차이가 0이면 내가 구한 해가 정답일 가능성이 높음
> 이 차이를 dual gap이라고 한다
> 라그랑주 함수의 최적값 d*는 프리멀 함수의 최적값 p* 보다 작거나 같음 왜냐하면 하한 값이기 때문.
> KKT 조건이 만족하면 duality gap이 0이 된다.
> 위의 식이 목적함수이다. 제약 조건이 없다.
> yi는 실제 타깃값, 뒤의 값은 예측값, 둘의 차이 즉 loss 임
> 제약 조건을 걸 수 있다.
> 최적화 방법을 옵티마이저라고 한다.
> 그 중 유명한 게 그래디언트 디센트다.
> 컴퓨터는 한 번에 미분값을 구하기 어렵기 때문에 여러 번 갈 곳을 찾아서 미분을 하고 갈 곳이 없을 때 정상이고 그 값을 찾는다.
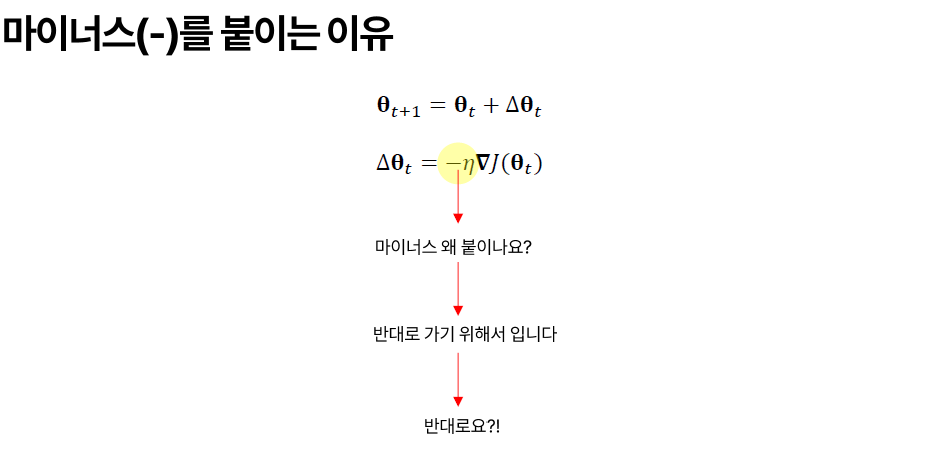
> 에타는 학습률을 의미한다.
> 직접 입력하는 값이다.
> 예를 들어 100이라는 값은 보폭률임, 커지면 빨리 도달함
> 단점은 정상을 지나쳐 버릴 수 있음
> 마이너스 붙는 이유는 가야되는 방향이 반대이기 때문.
> 한 걸음 걸을 때 마다 그래디언트를 구해야 함(전체 데이터에서)
> 연산량이 너무 많음
> 그래서 일부분을 채택하는 방식을 선택하게 됨.
> 확률적으로 샘플 뽑아서 연산을 하고 이를 SGD라고 한다.
> 장점을 빠르지만 outlier가 걸리면 한 걸음 아주 이상한 방향으로 갈 수 있다. (정확성 떨어짐)
> 그래서 정확도를 좀 더 올리기 위해 여러 데이터를 뽑는다.
> 일반적으로 많이 쓰기 때문에 이것을 SGD라고 한다.
> 데이터의 크게 두 가지가 있다 Batch / Streaming
> Batch는 데이터를 모아서 덩어리로 처리
> Streaming은 실시간으로 하나씩 처리
> 학습 속도를 가속화 하는 방법이 모멘텀이라고 한다.
모형 평가
> 단위가 다르면 비교가 어렵기 때문에 Scaling을 해야 한다
> 표준화하기 위해선 평균과 표준편차를 알고 있어야한다
> 데이터 표준화된 데이터를 학습시킨다
> 혼용하는 단어 standadization, normalization, regularization
> standardization : (원래 데이터 - 평균)/표준 편차 → 평균 0, 표준편차 1 :표준화
> normalization : 원래 데이터 / 원래 데이터의 크기 → 크기가 1 :노멀화
> regularization : 제약식을 넣는다. : 정규화
> 데이터가 0, 1 사이로 모이게 된다.
> 피쳐 별 Min, Max 값 알아야 한다.
> Standardization과 MinMax 차이는 범위다.
> outlier가 들어가면 그 값은 1이 되고 나머지 값은 0으로 수렴된다.
> 어떤 게 좋은지는 답은 없고 데이터 상황에 따라 다르다.
> 잘 만들어졌는지 확인하는 방법
> 다 병 걸렸다고 해버리면 치료율이 100% 로지만 정상인 사람들도 병에 걸렸다고 판단될 수 있다.
> 반대론 피해율 0%이다.
> 1종 2종 오류이다.
> 알고리즘 보단 평가지가 매우 중요하다.
> 민감도는 sensitivity보단 recall이란 단어를 많이 씀
> 병에 걸린 사람들 중 적중한 것이 recall
> 내가 병에 걸렸다고 한 사람들 모아 놓고 그중 맞춘 비율이 precision
> 어떤 것을 사용할지가 매우 중요.
> TP 1 FN1 FP 2 TN 96 이면 accuracy 0.97, 민감도 0.5 이런 상황에선 recall을 사용해야 한다.
> 이런 상황은 데이터 결과가 치우쳐진 경우
> 해커 판별 시 정상인이 정상인으로 판단하는 건 accuracy도 높음 해커들이 별로 없지만 결국 별로 의미 없음
> 데이터 벨런스가 잘 잡혀있으면 accuracy 써도 무방함.
> 대중적으로 많이 쓰는 건 accuracy랑 recall.
> MSE 범위는 0에서 무한대
> 단위를 맞추는 RMS, 절댓값의 합의 평균 MAE
> 녹색 점을 예측한다고 할 때 2가지가 있다고 가정해 보면
> MSE 기준 2번이 더 좋은 모델이다.
> 하지만 주어진 데이터에서 새로운 데이터를 맞추는 것이 목적이다
> 데이터가 달라진다고 하면 1번 모델이 더 적절하다
> 따라서 파란색 선이 오버피팅이라고 한다
> 오버피팅은 특정 형태만 잘 맞추는 모델이다.
> 적절한 모형보다 차수가 높아서 오버피팅이라고 한다.
> 오버피팅을 빠져나가기 힘들다 (MSE가 최소이기 때문에)
> MSE가 커서 걱정하다 MSE가 낮아짐 알고 보면 오버피팅의 경우가 많다.
> 평가 지표로만 판단하면 안 되고 그래프나 시각화를 통해 오버 피팅을 확인해야 한다.
> 2차원 보다 작은 1차원이기 때문에 언더 피팅이다.
> 못 맞추는 게 문제임
> 오버 피팅이 더 문제이다 왜냐하면 맞췄는지 못 맞췄는지 판단하기 어려움
> 학습시키고 나서 정답을 잘 맞히는지 확인을 못 함
> 그래서 학습을 1~8까지만 학습하고 모델을 만든 후 9, 10회로 잘 맞추는지 확인하는 개념이 교차 검증(Cross Validation)
> 새로운 데이터가 올 때까지 기다려야 하는데 시간적 여유가 없는 케이스가 많다
> Training Data만 학습시키고 Test Data는 학습에 사용하지 않는다
> 더 쪼갠다 Validation, (Validation Data)를 사용하지 않는 경우도 있다
> 5 등분해서 validation을 활용해서 데이터가 쏠리지 않게 validation 위치를 바꿔가면서 학습시키는 방법
> k는 등분 개수 5개
> 알고리즘 배울 때 Train/Test만 나눠서 함
> 비율은 8:2, 7:3 (라이브러리 디폴트 갑은 7.5 : 2.5)
> validation은 등분이라 상관없음
> 사용하는 라이브러리는 scikit-learn
> R은 모델마다 라이브러리를 써야 함
> 그래서 통합 라이브러리가 나왔는데 이 라이브러리도 또 여러 개임
> regression 회기, 연속형 데이터 예측
> clustering은 비지도 학습 classification 은 지도 학습
> dimensionality reduction 차원 축소
'Machine Learning 입문' 카테고리의 다른 글
| 9. 앙상블 학습 (2) | 2024.12.28 |
|---|---|
| 8. 지도 학습 (0) | 2024.12.26 |
| 6. 확률 분포 & 가설 검정 (0) | 2024.12.26 |
| 5. 데이터 전처리 처리 및 시각화 (0) | 2024.12.26 |
| 4. 기초 통계 & 시각화 (2) | 2024.12.26 |
- Total
- Today
- Yesterday
- 열전자 방출
- Fiber Optic
- Pinch Off
- C언어 #C Programming
- channeling
- Diode
- semiconductor
- 문턱 전압
- Solar cell
- EBD
- Blu-ray
- Thermal Noise
- 쇼트키
- PN Junction
- Laser
- Acceptor
- Donor
- 반도체
- Reverse Bias
- Depletion Layer
- pn 접합
- Charge Accumulation
- 양자 웰
- Semicondcutor
- fermi level
- Energy band diagram
- Optic Fiber
- MOS
- 광 흡수
- CD
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |