티스토리 뷰
res = 0
for i in range(0,11):
res += i
res
> res는 result의 약자
> 제곱의 Sigma (합)
res = 0
for i in range(1,6):
res = res + i**2
res
> 결과가 맞는지 확인하기 위해 print를 활용해서 중간값을 보여줘야 함
res = 0
for i in range(1,6):
res = res+ i**2
print(f'i는 {i}, res는 {res}')
print("________________")
res
> 제곱합이 중요한 이유는 그래프를 그리면 변곡점을 최적점으로 찾기 때문이다. 보통 2차 함수를 사용한다. 3차, 4차는 최적점을 찾기 어려움.
> 결국 미분에서 0이 되는 지점을 찾는 과정.
> 시그마의 곱 버전.
> 파이는 사건이 동시에 일어나는 확률을 계산할 때 활용.
res=1
for i in range(1,10):
res= res*i
res
def factorial(n):
res = 1
for i in range (1, n+1):
res *= i
return res
> 파이와 다른 점은 끝이 항상 1까지 고정이고 파이는 처음과 끝을 정할 수 있다.
def combination(n,x):
res=factorial(n)/factorial(x)*factorial(n-x)
return res
combination(3,5)
> 머신러닝에서 순열 Permitation은 안 씀
> 머신러닝에서 샘플링해서 돌릴 때 사용 됨.
x=13
if x < 10:
res = 1
else :
res= 0
res
> I(y=사과) 이면 사과이면 1, Sigma(I(y=사과)) 는 사과의 개수, 1/n(Sigma(I(y=사과))는 사과일 확률
> 예) yn (target의 n번째)가 ignore index 가 아니면 1
import numpy as np
x = range(1,10)
a =list(x)
np.argmin(a)
> 최솟값의 Index를 반환, argmax는 반대.
> 최솟값이 여러 개이면 맨 처음 Index를 반환.
> numpy에서 만든 64비트 정수형임, numpy가 가지고 있는 자료형이고 이게 있어야 연산이 빠름, 이런 형식으로 보기 싫을 땐 print로 하면 된다.
> 2차 함수의 x, y가 있으면 argmin은 x 값, min 값은 y.
> 머신러닝은 최적점인 argmin 값을 찾는 것이기 때문에 argmin 개념은 중요하다.
> ex) 돌고래, 고양이 구분하는 결과가 0.9, 0.1이라면 max는 0.9, argmax는 돌고래임. 돌고래를 구분하고 싶은 것이기 때문에.
> 좌극한 우극한이 같지 않으면 수렴하지 않는다
> 이차 함수 쓰는 이유는 끊어진 부분이 없기 때문.
> 머신러닝 관점에서 feature 변화에 따른 함수 값을 구할 때 미분 사용
> 미분해서 0되는 점이 최적점이다.
> 끊어지거나 꺾이는 점은 미분 불가하다. (절대값)
> 컴퓨터는 점을 이동하면서 접선을 구하고 0이 되면 멈춘다.
> 미분 공식을 사용하지 않기 때문에 절댓값도 사용하기도 한다.
> 다변수는 feature가 많다, 하나의 feature에 대한 변화율이 편미분이다.
> 여러 feature에 대한 편미분은 한 번에 표현한 것이 그레디언트
> 머신러닝 관점에선 그레디언트는 각 feature들의 편미분을 구해서 어디로 가야 할지 방향을 정한다.
> 깜깜한 밤에 산 정상을 올라갈 때 한 발자국씩 디뎌서 경사도 가장 가파른 곳을 선택하는 것처럼
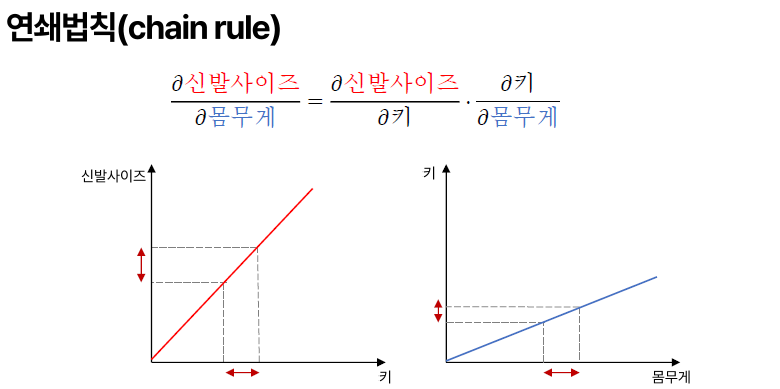
> 몸무게와 신발 사이즈 관계가 없고 신발, 키와 키와 몸무게 관계를 알고 있을 때 곱하면 알 수 있다.
> 머신 러닝에서 적분이 필요한 이유는 확률을 구하기 위함.
> 확률 분포(정규 분포)의 넓이를 구하면 확률임.
> 손으로 적분이 안 되는 것들을 이제 컴퓨터로 구분 구적법을 이용한 것이 몬테카를로 방법임.
> 마르코프 체인 몬테카를로 MCMC 방법도 있다.
> 통계에선 두 가지 파 빈도학파, 베이지안 파가 있음.
> 이전 데이터 기록을 활용해서 예측은 빈도학파 (클래식)
> 베이지안은 여러 feature를 활용해서 상태 변화를 예측?
> 생성모형, GAN, Chat GPT에 베이지안 활용한다.
'Machine Learning 입문' 카테고리의 다른 글
| 6. 확률 분포 & 가설 검정 (0) | 2024.12.26 |
|---|---|
| 5. 데이터 전처리 처리 및 시각화 (1) | 2024.12.26 |
| 4. 기초 통계 & 시각화 (2) | 2024.12.26 |
| 3. 선형 대수 (0) | 2024.12.24 |
| 1. 가상 환경 Setting / Jupyter Notebook (0) | 2024.12.24 |
- Total
- Today
- Yesterday
- Solar cell
- MOS
- Laser
- PN Junction
- Blu-ray
- 양자 웰
- 열전자 방출
- CD
- Charge Accumulation
- pn 접합
- Diode
- Reverse Bias
- Semicondcutor
- C언어 #C Programming
- Thermal Noise
- Acceptor
- 쇼트키
- Pinch Off
- fermi level
- Depletion Layer
- channeling
- EBD
- 광 흡수
- 문턱 전압
- 반도체
- Fiber Optic
- Energy band diagram
- Optic Fiber
- Donor
- semiconductor
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |